Julia 笔记系列：

唠唠闲话

本篇介绍 Julia 的类型，派发与设计模式，对应课程第三讲，主要内容：

官方文档：类型，方法，性能建议，风格建议。

类型与派发

本节介绍 Julia 的几种数据类型：

类型名 定义关键字 说明
具体类型 struct 可以被实例化
可变类型 mutable struct 属于具体类型，但数据可变
抽象类型 abstract type 不能实例化，常用于标记数据类型
参数化类型 关键字 + {} 允许更多类型可能性

并介绍类型的三个应用：

具体类型与实例化

  1. 具体类型用关键字 struct 定义，比如

    1
    2
    3
    4
    struct Point2D <: Any
        x::Float64
        y::Float64
    end

  2. 定义说明：

    • 类型名称为 Point2D
    • <: 表示继承关系，第一行表明新类型 Point2D 为 Any 子类
    • Julia 中所有类型都是 Any 子类，因此 <: Any 可以略写
    • 函数外使用 <: 或 >: ，可以判断两个类型是否有继承关系
    • :: 用于声明变量类型，比如 x::Float64 声明变量 x 的类型为 Float64
    • 直接写 x 等同与 x::Any

  3. 下边三种实例化方法的结果等价

    1
    @info "三种输入的实例化结果等价" Point2D(1,2) Point2D(1.0,2.0) Point2D(1,2.0)

    深度截图_选择区域_20211101113002

  4. 定义背后实际运行了下边代码

    1
    2
    3
    4
    5
    6
    7
    8
    struct Point2D
        x::Float64
        y::Float64
        function Point2D(x::Float64, y::Float64)
            new(x, y)
        end
        Point2D(x, y) = Point2D(Float64(x), Float64(y))
    end
    • 输入 Int64 类型数据
    • 调用第 7 行的函数，将输入数据转为 Float64 类型
    • 调用第 4 行的函数，创建结构体

  5. 结构体内部数据用点号获取，比如
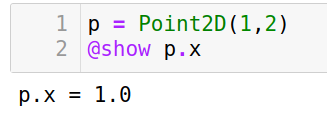
    深度截图_选择区域_20211101113542

  6. 结合类型派发，可以灵活定义实例化，比如

    1
    Point2D(x) = Point2D(x,zero(x))

    设置 Point2D 第二参默认值为 0，其中函数 zero(x) 返回 x 类型相同的零元。

  7. 上篇介绍的Julia 数据类型中 Float64 为具体类型， Any 为抽象类型。判断数据类型用函数 isconcretetype 和 isabstracttype 。

    1
    2
    @info "具体类型" isconcretetype(Float64) isabstracttype(Float64)
    @info "抽象类型" isconcretetype(Real) isabstracttype(Any)

    深度截图_选择区域_20211101112737

关于动态类型
Julia 是一种动态类型的语言：

  • 当数据类型不确定时，Julia 用类似 Python 解释器的方法运行代码，计算效率低。
  • 当数据类型确定时，Julia 通过编译或调用更高效的方法运行代码。

如果希望编译器运行更快，编写时应尽可能告诉系统数据的类型信息，让系统能使用更高效的方法来运行代码。

可变类型

  1. struct 定义的数据类型，实例化后不能修改内部数据，否则报错

    1
    2
    p = Point2D(1, 3)
    p.x = 0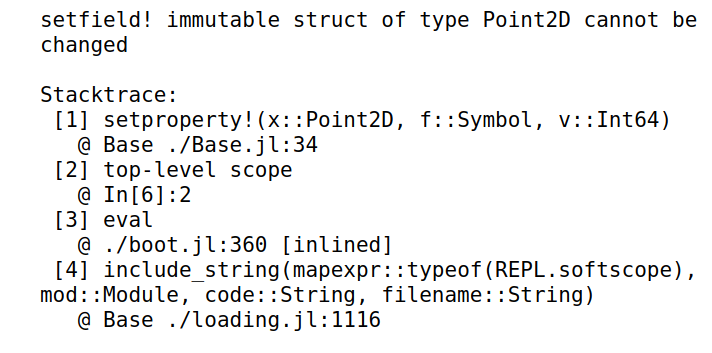

    20211101150445

  2. 如果要修改内部数据，可以加关键字 mutable 使数据类型可变

    1
    2
    3
    4
    5
    6
    7
    8
    mutable struct MPoint2D
      x::Float64
      y::Float64
    end
    p = MPoint2D(2.0, 1.0)
    @show p
    p.x = 0
    @show p

    20211101150726

注：可变数据不能直接存放在寄存器和栈中，会让代码性能变慢，应尽量避免使用。

抽象类型，继承和类型树

抽象类型用关键字 abstract type 定义

1
abstract type AbstractPoint <: Any end

<: Any 表示 AbstractPoint 为 Any 的子类，可略写。

抽象类型和具体类型有以下区别：

  1. 抽象类型可被继承，作为父类型，而具体类型不能被继承，比如

    1
    2
    3
    4
    5
    6
    7
    # 抽象类型 <: 抽象类型
    abstract type AbstractPoint2D <: AbstractPoint end
    # 具体类型 <: 抽象类型
    struct NewPoint2D <: AbstractPoint
        x::Float64
        y::Float64
    end

    下边代码将报错

    1
    2
    3
    4
    struct SubPoint2D <: NewPoint2D
        x::Float64
        y::Float64
    end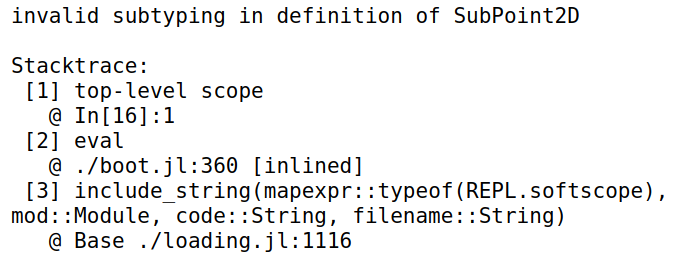

    深度截图_选择区域_20211101152428

  2. 具体类型可以实例化，而抽象类型不能实例化，下边代码将报错

    1
    2
    3
    4
    abstract type AbstractPoint
        x::Float64
        y::Float64
    end

  3. 抽象类型结合函数方法也可以创建“实例”

    1
    2
    AbstractPoint(x, y) = NewPoint2D(x, y)
    @show AbstractPoint(1,2)

    注意这里实际上是调用了 NewPoint2D 的实例化
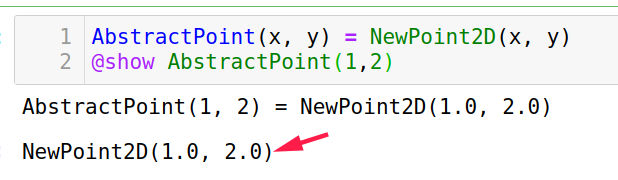
    深度截图_选择区域_20211101153042

  4. 用子节点表示继承关系，具体类型和抽象类型可以用类型树来理解
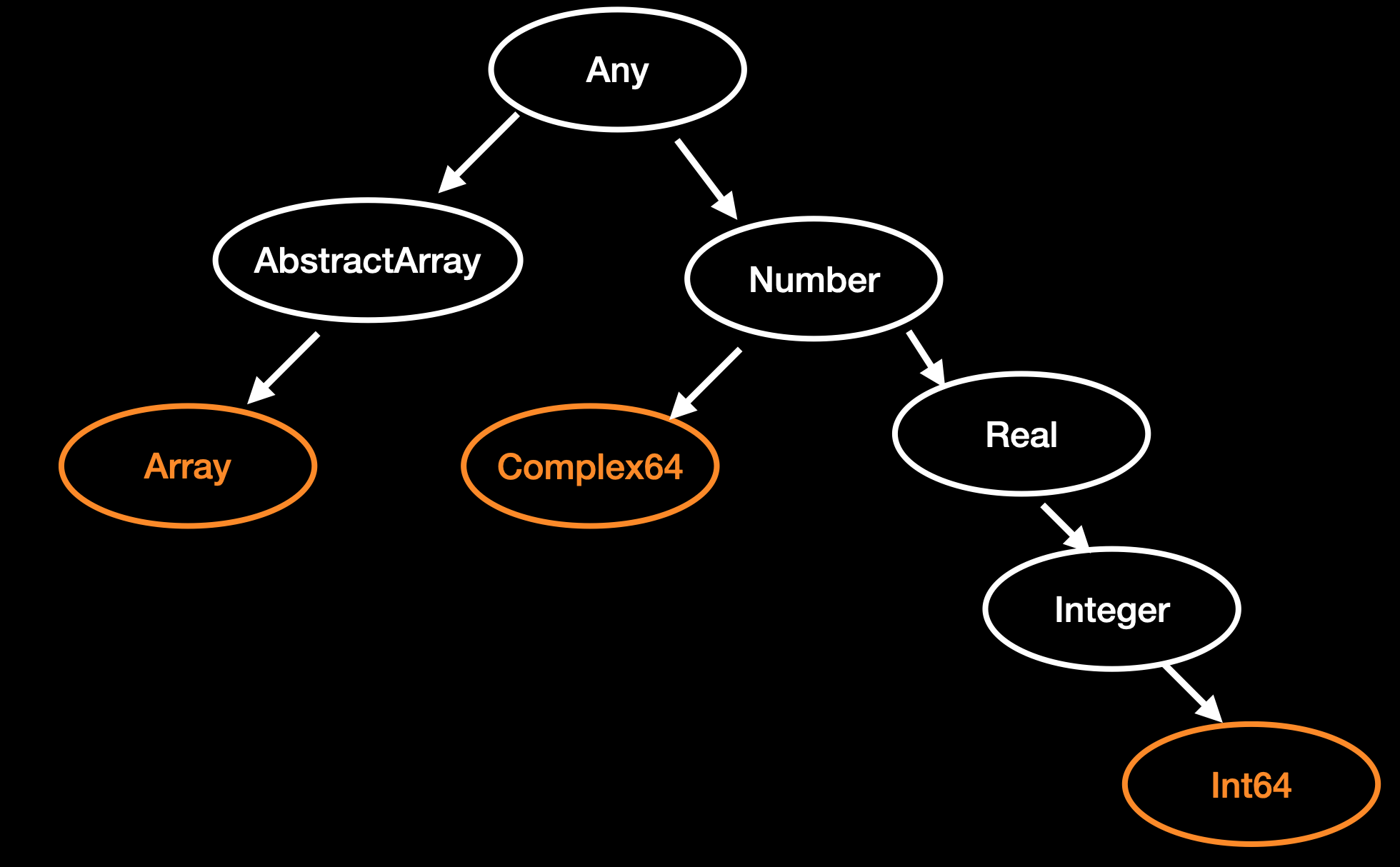
    20211101153336

    • 具体类型不能被继承，可以实例化，对应图中橙色部分，只能作为叶子节点
    • 抽象类型可以被继承，不能实例化，对应图中白色部分，可以往下连接节点

官方文档：抽象类型形成了概念的层次结构，这使得 Julia 的类型系统不仅仅是对象实现的集合。

参数化类型

回顾具体类型 Point2D 的定义

1
2
3
4
struct Point2D <: Any
    x::Float64
    y::Float64
end

Point2D 的内部数据 x 和 y 的类型固定为 Float64。类型一旦定义，就不能修改了。但一些时候，我们希望 x 和 y 能设置多种类型，以应对不同场景。这时可以用参数化类型(parametric composite type)来实现。

  1. 使用 {} 定义参数化类型

    1
    2
    3
    4
    struct Point{T<:Real} 
        x::T
        y::T
    end

    定义说明：
    - 定义参数化类型 Point{T}，内部变量 x 和 y 的类型为 T
    - T 为类型变量， T<:Real 限定 T 的取值为实数 Real 的子类

  2. 用三种方法实例化，第一种得到具体类型 Point{Float64}，后两种得到 Point{Int64}

    1
    2
    @info "三种实例化方法" Point(1.0,2.0) Point(1,2) Point{Int64}(1.0,2)
    # 第三种如果直接输入混合类型 Point(1.0,2) 将报错

    深度截图_选择区域_20211101161237

  3. 注意参数化类型 Point 不是严格意义的类型(DataType)，仅当变量 T 确定时，Point{T} 为类型，比如 Point{Int64}

    1
    @info "参数化类型 vs 类型" typeof(Point) typeof(Point{Int64}) typeof(Point2D) typeof(AbstractPoint)

    深度截图_选择区域_20211101161052

  4. 参数化类型 Point 在实例化时，背后实际运行了：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    struct Point{T<:Real}
        x::T
        y::T
        
        function Point{T}(x::T, y::T) where T <: Real
            new{T}(x, y)
        end
        function Point(x::T, y::T) where T <: Real
            Point{T}(x, y)
        end
    end

    where 按英文意思理解，当 T <: Real 即 T 为 Real 子类时，调用该方法。

  5. 抽象类型也可以参数化，比如

    1
    abstract type AbstractPoint{X,Y} end

    参数化抽象类型 AbstractPoint ， X 和 Y 为待定类型，用法在典型设计中进一步介绍。

关于 where

  1. where 为中缀运算符，用于编写参数方法和类型定义。where 前接类型变量，后接类型限定，比如

    1
    @show typeof(Point{T} where T <: Real)

    where 表明左侧的 T 为变量，右侧限定 T 为 Real 子类。整个表达式的类型为 UnionAll，可以理解为类型的集合体。
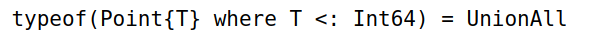
    深度截图_选择区域_20211103172145

  2. where 后边的限定只能用继承关系 <: 和 >:，不能使用 == 之类的判断

    1
    2
    3
    4
    # 输入正常
    Point{T} where T <: Float64
    # 输入报错
    Point{T} where T == Float64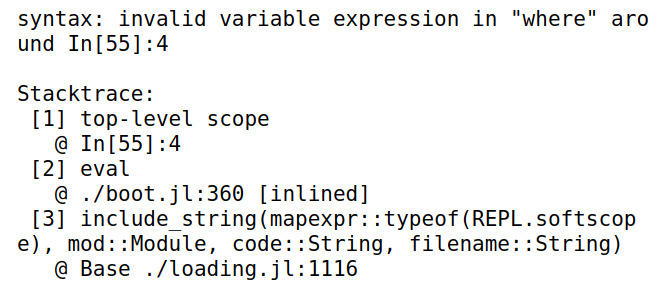

    深度截图_选择区域_20211103212632

  3. 嵌套的 where 表达式有简洁的写法

    1
    2
    3
    # 下边方法等价
    Pair{T, S} where S<:Array{T} where T<:Number
    Pair{T, S} where {T<:Number, S<:Array{T}}

  4. where 可用于获取输入数据的类型，比如

    1
    my_typeof(::T) where T = "Data type is $T"

    深度截图_选择区域_20211103174632

类型的三个应用

多重派发

  1. 函数允许定义多种方法，调用时，调用类型“最具体”的方法

    1
    2
    3
    4
    g(x) = "Any"
    g(x::Real) = "Real"
    g(x::Int64) = "Int"
    @info "几种调用方法" g("str") g(1.0) g(1)

    深度截图_选择区域_20211101165432

  2. 存在多个匹配且无法判断时直接报错

    1
    2
    3
    4
    h(x, y) = "h(x::Any, y::Any) is called"
    h(x, y::Number) = "h(x::Any, y::Number) is called"
    h(x::Number, y) = "h(x::Number, y::Any) is called"
    @show h(1, 1.0)

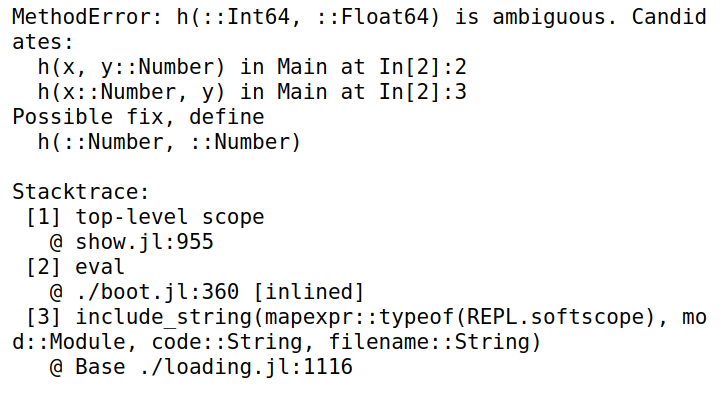
    20211101165556

  3. 出现歧义时，一般通过补充定义来辅助类型判断

    1
    2
    h(x::Number, y::Number) = "h(x::Number, y::Number) is called"
    @show h(1, 1.0)

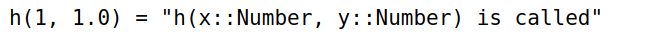
    深度截图_选择区域_20211101165708

  4. 关键字不参与多重派发

    1
    2
    3
    4
    f(x;y=1)=x+y
    @show f(2)
    f(x) = x # 函数重载，覆盖旧定义
    @show f(2)

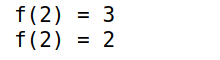
    深度截图_选择区域_20211101170002

函子

我们函数 f(x) 的 f 称为“函数名变量”，x 称为函数变量；Julia 的多重派发不仅可以对函数变量进行，还可以对函数名变量进行，效果类似 Python 里的 __call__ 方法

比如定义参数化类型 Format，用于将浮点数化整数

1
2
3
4
struct Format{T<:Integer} end
(func::Format{T})(a::Float64) where T = T(floor(a))
int32 = Format{Int32}()
int32(1.2) # 输出结果为 1

再比如一个稍复杂点的例子：

  1. 定义函数 f：判断元素 x 是否在区间 [a,b] 上

    1
    2
    3
    4
    f(x,a,b) = a ≤ x ≤ b # 判断 x 是否在 [a,b] 上
    a,b = 3,7
    data = rand(1:10,5)
    @show f.(data,a,b)

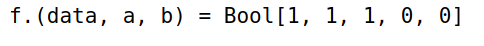
    深度截图_选择区域_20211101171439

  2. 我们希望每次输入 a 和 b，就得到一个判断函数

    1
    2
    3
    4
    5
    struct MinMax
        min::Int64
        max::Int64
    end
    (func::MinMax)(x)=func.min ≤ x ≤ func.max

    1-4 行定义结构类型
    最后一行对函数名变量派发，当左侧 func 的数据类型为 MinMax 时，执行右侧运算。

  3. 原先的调用方式 f.(data,a,b) ，现在改为

    1
    2
    inrange = MinMax(3,7) # 实例化
    @show inrange.(data)

    20211101172943

  4. 通过对“函数名变量”的派发，具体类型 MinMax 的每次实例化，都得到一个函数。

  5. Julia 的多重派发类似于 Mathematica 的上下值；上值 UpValues 针对函数名变量，下值 DownValues 针对函数参数。

Ps：不清楚为什么叫函子，和范畴里的函子定义有什么联系？

“类编程”

Python 类(class) 的一些功能可以用 Julia 的结构体(struct) 实现。比如类对象的等号判断 __eq__ ，在 Julia 中可通过修改算符 == 实现。

  1. 定义结构类型 Point

    1
    2
    3
    4
    struct Point{T<:Real} 
        x::T
        y::T
    end

  2. 实例化类型为 Int32 和 Int64 的两个点，默认情况下，类型不同的数据认为不相等

    1
    2
    3
    @show p1 = Point(1,2)
    @show p2 = Point{Int32}(1,2)
    @show p1 == p2

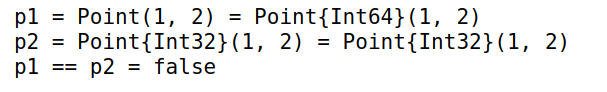
    深度截图_选择区域_20211103150936

  3. 修改符号 == 的定义，在判断相等时忽略类型

    1
    2
    Base.:(==)(p::Point, q::Point) = p.x == q.x && p.y == q.y
    @show p1 == p2

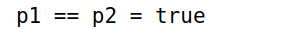
    20211103151334

注意 == 是Julia 的基础函数模块 Base 中的函数，修改模块函数要用 PkgName.funName 的方法。

  1. 比如直接修改 Base 中的函数 print 将报错

    1
    2
    3
    function print(p::Point)
        print("($(p.x), $(p.y))")
    end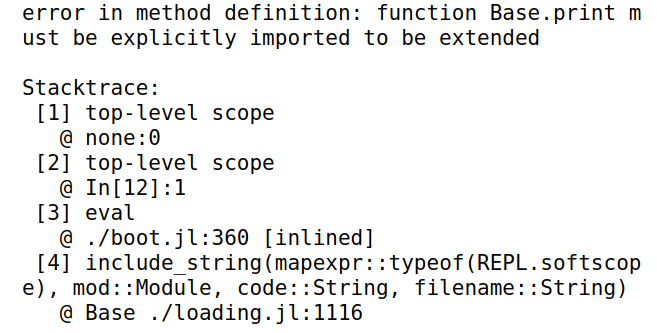

    20211103151851

  2. 正确修改方法为：

    1
    2
    3
    function Base.print(p::Point)
        print("($(p.x), $(p.y))")
    end

  3. 此外，修改算符要用 :(算符) ，否则报错

    1
    2
    3
    4
    function Base.:(+)(p1::Point,p2::Point)
        Point(p1.x + p2.x, p1.y + p2.y)
    end
    @show p1 + p2

    深度截图_选择区域_20211103152438

典型设计模式

本节介绍 Julia 代码的设计模式，这些在 Julia 标准库中随处可见，核心思路是：

  • 设计更一般化的代码来支持不同的使用
  • 达到最佳性能

代码设计

特征函数

  1. eltype, typeof, ndims 等用来提取一些基本信息的函数在 Julia 称为特征函数(trait function)。

  2. 数组 Array 和向量 Vector 继承于抽象类型 AbstractArray

    1
    2
    @show Vector <: AbstractArray
    @show Array <: AbstractArray{T,N} where {T,N}

    深度截图_选择区域_20211103214447
    这里 AbstractArray 的两种写法等价

  3. 查看向量 x=[1,2,3] 的类型特征

    1
    2
    3
    4
    5
    x = [1,2,3]
    @show typeof(x)
    @show typeof(x) <: AbstractArray
    @show eltype(x)
    @show ndims(x)

    深度截图_选择区域_20211103214120

  4. 数组类型 Array 继承于 AbstractArray，我们可以利用 where 语法规则，编写类似 typeof, eltype 和 ndims 的函数

    1
    2
    3
    4
    5
    6
    my_typeof(::T) where T = T
    my_eltype(::AbstractArray{T}) where T = T
    my_ndims(::AbstractArray{_,N}) where {_,N} = N
    @show my_typeof(x)
    @show my_eltype(x)
    @show my_ndims(x)

    深度截图_选择区域_20211103214842

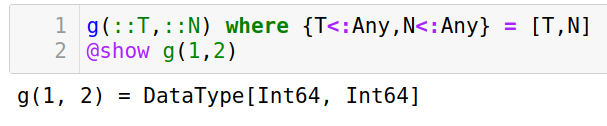
  5. 当我们只关心输入类型，而不关心输入数据，变量名可以略写，比如
    深度截图_选择区域_20211103222456

Holy-trait

  1. Julia 中的类型不允许继承于多个抽象类型，比如

    1
    2
    3
    4
    5
    abstract type Flyable end
    abstract type Bird end
    struct Penguin <: {Flyable, Bird}
        name
    end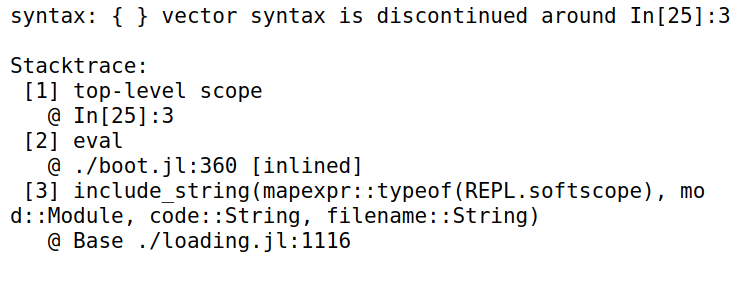

    深度截图_选择区域_20211103221303

  2. 假设对函数做多重派发，我们希望当数据同时属于两个类型时执行函数，这时可以构造空数据类型来实现，这种方法称为 Holy-trait，发明者为 Tim Holy。

  3. 举个例子，定义两个类型 Parrot 和 Penguin，类型先继承于鸟类，然后分别伪“继承”于会飞 Flyable 和不会飞 NotFlyable 。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    ## 定义类型
    struct Flyable end
    struct NotFlyable end
    abstract type Bird end
    ## 定义动物，先继承 Bird 属性
    struct Parrot <: Bird
        name
    end
    struct Penguin <: Bird
        name
    end
    ## 借助函数，伪“继承” Flyable 属性
    is_flyable(::Penguin) = NotFlyable()
    is_flyable(::Bird) = Flyable()

  4. 定义函数 fly ，按变量类型是否同属于 Flyable 和 Bird 进行派发

    1
    2
    3
    4
    5
    fly(x) = fly(is_flyable(x), x::Bird)
    fly(::Flyable, x::Bird) = "$(x.name) flys"
    fly(::NotFlyable, x::Bird) = "$(x.name) can't fly"
    @show fly(Penguin("Jane"))
    @show fly(Parrot("Doe"))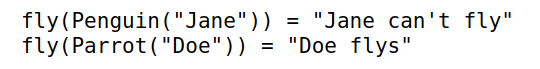

    深度截图_选择区域_20211103223332

这里第一个函数 fly 检查输入变量 x 是否继承于 Bird，然后第2，3个函数 fly 根据是否继承于 Flyable 进行派发。

这在某些场景下非常有用，例如有时我们需要检查：

  1. 数据类型为矩阵子类
  2. 数据类型支持线性下标索引

关键点在于，线性下标索引允许更高效的内存操作，但我们不能在代码运行时通过 if 来检查输入的矩阵类型是否支持线性下标索引，因为这会浪费计算量，且 if 语法的出现会导致编译器无法给出高效的代码优化（例如 SIMD）。
当然，初学并不需要思考这些特别基础的东西，但是如果想要进一步提升编程的认知并且成为一个开发者的话，这些是需要了解的。

代码性能

提供类型信息

不考虑算法层面的话，在 Julia 下想得到更好性能的核心思路就是：传递更多的类型信息给编译器。

  1. 用相同方法定义函数，方法一向编译器提供信息，方法二不提供。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    ## 定义函数一
    function my_sum_1(X)
        rst = zero(eltype(X))
        @inbounds @simd for x in X
            rst += x
        end
        return rst
    end
    ## 定义函数二
    function my_sum_2(X)
        rst = zero(eltype(X))
        for x in X
            rst += x
        end
        return rst
    end

  2. 测试速度

    1
    2
    3
    X = rand(1000)
    @btime my_sum_1(X)
    @btime my_sum_2(X)

    20211103225004

  3. 二者运行时间相差明显，这里方法一加快是因为使用了两个宏命令：

    • @inbounds 表示右边 for 循环的内容不会超出索引，运行时不用检查
    • @simd 用并行计算给运算加速

类似地，提供数据类型可以加快运算

  1. 定义函数和数据类型

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    function my_sum(X)
        rst = eltype(X)(0)
        @inbounds @simd for x in X
            rst += x
        end
        return rst
    end
    # 两种数据类型
    struct NumAny x end
    struct NumFloat x::Float64 end
    # 重定义内置函数
    Base.:(+)(a::NumAny,b::NumAny) = NumAny(a.x + b.x)
    Base.:(+)(a::NumFloat,b::NumFloat) = NumFloat(a.x + b.x)
    Base.zero(::NumAny) = NumAny(0)
    Base.zero(::NumFloat) = NumFloat(0)

  2. 对比时间

    1
    2
    3
    4
    X = @btime [NumAny(rand()) for _ in 1:100]
    Y = @btime [NumFloat(rand()) for _ in 1:100]
    @btime my_sum($X)
    @btime my_sum($Y)

    深度截图_选择区域_20211103233047

  3. 不指定类型，内存分配更多，用时更长，计算求和使用的时间更长，大约是后者的 200 倍。

类型稳定

考虑下边两个函数，一个输出结果稳定，一个不稳定

1
2
3
4
5
6
7
rand_unstable() = rand() > 0.5 ? rand(Int) : rand(Float64)
rand_stable() = rand() > 0.5 ? rand(Float64) : rand(Float64)

X = @btime [rand_unstable() for _ in 1:1000]
Y = @btime [rand_stable() for _ in 1:1000]
@btime my_sum_1($X)
@btime my_sum_1($Y)

深度截图_选择区域_20211103230413

注意时间单位，不稳定类型在运算中分配的内存更多，初始化时间长，运行效率低。

Julia 编译器会自动判断代码输出类型是否稳定。查看输出类型可使用宏 @code_warntype，比如

1
2
@code_warntype rand_unstable() 
@code_warntype rand_stable()

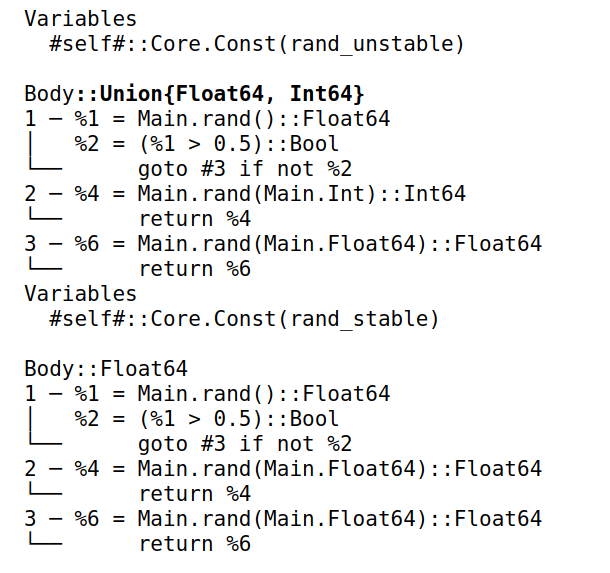
深度截图_选择区域_20211104093155

可补充

  1. 实例化 p.x 与 getfield(p,x)
  2. 结构体内定义的函数
  3. 结构体内的 new
  4. 函子和范畴函子的联系
  5. 深度学习，以及上一讲的梯度下降