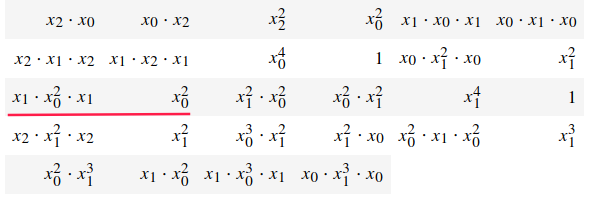Weyl 群扩张群的结构 | SageMath 实战

唠唠闲话

本篇用 GAP 和 SageMath 研究 Weyl 群扩张群的结构，顺带演示编程能做什么样的任务，以及是怎么完成的。

内容安排如下：

• 记号及问题
• $\widetilde{W}的结构$
• $\widetilde{W}$的泛性质
• 总结及延伸

---

记号，问题及结论

记号和问题

1. 符号和定义

   $$\begin{array}{|c|c|c|} \hline 符号 & 定义 & 补充\\\hline L&复数域上半单李代数& -\\\hline H&Cartan 子代数 & -\\\hline S&单反射集 & S=\{s_i\}_{i=1}^n\\\hline W=\langle S\rangle&Weyl 群 & -\\\hline A&Cartan 矩阵 & A=(A_{ij})_{n\times n}\\\hline (\Phi,\Pi)&根系和单根系 & -\\\hline \{e_i,f_i,h_i\}_{i=1}^n& L 的代数生成元 & -\\\hline Der(L)&导子代数 & -\\\hline e^\delta,\delta\in Der(L)& 幂零导子诱导同构 & e^\delta:=\sum\limits_{k=0}^\infty \frac{1}{k!}\delta^k\\\hline Inn(L)&内自同构群 & 由 e^{adx} 生成，x\in L 且 adx 幂零\\\hline \end{array}$$

   特别地，由于伴随作用 $ade_i,adf_i$ 为幂零导子，定义内自同构

   $$\theta_i=e^{ade_i}e^{-adf_i}e^{ade_i}$$

   记 $\theta_i$ 生成的群为 $\widetilde{W}$，即

   $$\widetilde{S}=\{\theta_i\}_{i=1}^n,\ \widetilde{W}=\langle \widetilde{S}\rangle$$

2. $\widetilde{W}$ 的群结构是本篇的研究内容，具体地，从 $Weyl$ 群半直积角度与自由群商两个角度进行讨论。

3. 定义内自同构子群 $\widetilde{W}$ 到 Weyl 群的映射 $\varphi$：

   $$\begin{aligned} \varphi : Inn(L)&\rightarrow W\\ \tilde{w}&\mapsto \left.\tilde{w}\right|_H \end{aligned}$$

   由 Carter prop.7.18 知，$\varphi$ 为满的群同态且 $\varphi(\theta_i)=s_i$

4. 记群同态的核 $\widetilde{K}=ker(\varphi)$，则有

   $$\widetilde{W}/\widetilde{K}\cong W, \ \widetilde{W}\cong\widetilde{K}\rtimes_\sigma W$$

主要结论

1. $\widetilde{W}\cong K\rtimes_\sigma W$， $K$ 和 $W$ 如下表

   $$\begin{array}{|c|ccccccccc|} \hline type&A_n&B_n&C_n&D_n&E_6&E_7&E_8&F_4&G_2\\\hline K&(C_2)^{2\lfloor\frac 12n\rfloor}&(C_2)^{n-1}&(C_2)^{n-1}&(C_2)^{2\lfloor\frac 12(n-1)\rfloor}&(C_2)^{6}&(C_2)^{7}&(C_2)^{8}&(C_2)^{4}&(C_2)^{2}\\\hline W&S_{n+1}&(C_2)^n\rtimes S_n&(C_2)^n\rtimes S_n&(C_2)^{2\lfloor\frac 12(n-1)\rfloor}\rtimes S_n&-&-&-&-&D_{2\cdot 6}\\\hline \end{array}$$

   一般地，$K\cong (C_2)^{k_n}$，$k_n$ 为 Cartan 矩阵 $Z_2$ 列空间的维数

2. $\widetilde{W}$ 关于生成元 $\widetilde{S}$ 的泛性质为

   $$\begin{align*} (\theta_i\theta_j)^{o(s_is_j)}&= \begin{cases} \theta_i^2,& i=j\\ \theta_i^2\theta_j^2,& i\neq j,o(s_is_j)=2\\ \theta_i^2,& i\neq j,o(s_is_j)\neq 2,\vert\alpha_i\vert=\sqrt 2\vert\alpha_j\vert\\ 1,& otherwise \end{cases}&(1)\\ \theta_j\theta_i^2\theta_j^{-1}&=\begin{cases} \theta_i^2\theta_j^2& A_{ij}\ is\ odd\\ \theta_i^2& A_{ij}\ is\ even \end{cases}&(2)\\ \theta_i^2\theta_j^2&=\theta_j^2\theta_i^2,\ \forall\ i,j&(3)\\ \theta_1^{2\epsilon_1}\theta_2^{2\epsilon_2}\cdots\theta_n^{2\epsilon_n}&=1,\ (\epsilon_1,\epsilon_2,\cdots,\epsilon_n)A=0&(4) \end{align*}$$

---

$\widetilde{W}的结构$

先由编程实验获取规律和思路，再推导证明。

编程实验

1. 易证幂零导子有如下性质，这一性质将用于 $\theta_i$ 的计算

   $$(ade_i)^k=0\Leftrightarrow (adf_i)^k=0\Leftrightarrow k > \max_{j\neq i}\{-A_{ij},2\}$$

   特别地，对 ABCDEF 族单李代数：

   $$(ade_i)^3=0,\ e^{ade_i}=1+ade_i+\frac{1}{2}(ade_i)^2$$

   G 族单李代数：

   $$(ade_i)^4=0,\ e^{ade_i}=1+ade_i+\frac{1}{2}(ade_i)^2+\frac{1}{3!}(ade_i)^3$$

2. 由于 $\left.\theta_i^2\right|_H=\left.id\right|_H$ ，记 $K$ 为 $\theta_i^2$ 生成的 $\widetilde{W}$ 子群，则

   $$K =\langle\theta_i^2\vert i=1,\dots,n\rangle\subseteq\widetilde{K}$$

3. 计算观察 $\widetilde{W},K,W$ 三者关系，以 A 型为例

   # 导入自编函数 Thetas
   load("../src/weyl_group_extension.sage")
   # compare G,W and K
   res = [['level','|G|','|W|','|K|','Structure of G','Structure of W','Structure of K']] 
   s = "A" # Lie algebra of type A
   for n in range(1,8):
      thetas = [gap(mat) for mat in Thetas(s,n,reduced=True)]
      G = gap.Group(thetas)
      K = gap.Group([x^2 for x in thetas])
      W = WeylGroup([s,n])
      res.append([n, gap.Size(G), W.order(), gap.Size(K),
                  gap.StructureDescription(G), W.structure_description(), gap.StructureDescription(K)])
   table(res)

   $$\begin{array}{|c|cccccc|} \hline Type&|G|&|W|&|K|&Structure of G&Structure of W&Structure of K\\\hline A_1&2&2&1&C_2&C_2&1\\\hline A_2&24&6&4&S_4&S_3&C_2 \times C_2\\\hline A_3&96&24&4&(C_2 \times C_2) : S_4&S_4&C_2 \times C_2\\\hline A_4&1920&120&16&(C_2 \times C_2 \times C_2 \times C_2) : S_5&S_5&C_2 \times C_2 \times C_2 \times C_2\\\hline A_5&11520&720&16&((C_2 \times C_2 \times C_2 \times C_2) : A_6) : C_2&S_6&C_2 \times C_2 \times C_2 \times C_2\\\hline A_6&322560&5040&64&(C_2 \times C_2 \times C_2 \times C_2 \times C_2 \times C_2) : S_7&S_7&C_2 \times C_2 \times C_2 \times C_2 \times C_2 \times C_2\\\hline A_7&2580480&40320&64&((C_2 \times C_2 \times C_2 \times C_2 \times C_2 \times C_2) : A_8) : C_2&S_8&C_2 \times C_2 \times C_2 \times C_2 \times C_2 \times C_2\\\hline \end{array}$$

4. 容易发现以下规律：

   1. $K=\widetilde{K}$
   2. $K\cong (C_2)^{k_n}$ 为交换 p-群
   3. 归纳发现，$K$ 的结构有如下规律

   $$\begin{array}{|c|ccccccccc|} \hline type&A_n&B_n&C_n&D_n&E_6&E_7&E_8&F_4&G_2\\\hline K=\widetilde{K}&(C_2)^{2\lfloor\frac 12n\rfloor}&(C_2)^{n-1}&(C_2)^{n-1}&(C_2)^{2\lfloor\frac 12(n-1)\rfloor}&(C_2)^{6}&(C_2)^{7}&(C_2)^{8}&(C_2)^{4}&(C_2)^{2}\\\hline W&S_{n+1}&(C_2)^n\rtimes S_n&(C_2)^n\rtimes S_n&(C_2)^{2\lfloor\frac 12(n-1)\rfloor}\rtimes S_n&-&-&-&-&D_{2\cdot 6}\\\hline \end{array}$$

理论推导

下边推导 $K$ 的结构，解释上表规律，计算参看以前的录课或草稿文件。

1. 记 $k=A_{ij}(i\neq j)$，易证

   $$adf_i^sade_i^re_j=\begin{pmatrix}r\\ s\end{pmatrix}\begin{pmatrix}k-r+s\\ s\end{pmatrix}s!ade_i^{r-s}e_j\\ ade_i^sadf_i^rf_j=\begin{pmatrix}r\\ s\end{pmatrix}\begin{pmatrix}k-r+s\\ s\end{pmatrix}s!adf_i^{r-s}f_j$$

   继而得到 $\theta_i$ 作用公式：

   $$\begin{aligned} \theta_ie_j&=\begin{cases} \frac{1}{k!}(ade_i)^ke_j,& i\neq j\\ -f_i,&i=j \end{cases}\\ \theta_if_j&=\begin{cases} \frac{(-1)^k}{k!}(adf_i)^kf_j,& i\neq j\\ -f_i,&i=j \end{cases}\\ \end{aligned}$$

2. 推论1：记 $k=A_{ij}$，则

   $$\theta_i^2e_j=(-1)^ke_j\\ \theta_i^2f_j=(-1)^kf_j$$

3. 推论2：令 $\tau\in Aut(L)$ 如下定义，则有

   $$\tau(e_i)=-f_i,\ \tau(f_i)=-e_i,\ \tau(h_i)=-h_i\\ \tau\theta_i\tau=\tau\theta_i\tau^{-1}=\theta_i,\ \forall\ i$$

4. 推论3：$\forall\ w\in\widetilde{W}$，$w$ 被其在 $\{e_i\}_{i=1}^n$ 上的像确定。

5. 特别地，由于

   $$(\theta_i^2e_1,\theta_i^2e_2,\cdots,\theta_i^2e_n)=((-1)^{-A_{i1}}e_1,(-1)^{-A_{i2}}e_2,\cdots,(-1)^{-A_{in}}e_n)$$

   得到嵌入映射 $\psi$

   $$\begin{aligned} \psi :K&\hookrightarrow (C_2)^n\\ \theta_i^2&\mapsto row_i(A) \end{aligned}$$

   容易验证 $\psi$ 为群同态

   $$\psi(\theta_i^2\cdot\theta_j^2)=\psi(\theta_i^2)+\psi(\theta_j^2)\\$$

   故 $K$ 同构于 Cartan 矩阵的 $\mathbb{Z}_2$ 行空间的加法群，也解释了前边表格的规律

   $$K\cong Im(\psi)\cong span_{\mathbb{Z}_2}\{row_i(A)|\ \forall\ i\}$$

6. 举个例子， $A_3$ 的 Cartan 矩阵秩为 2， $K\cong (C_2)^2$

   $$\left(\begin{array}{rrr} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \end{array}\right)\overset{\mathbb{Z_2}}{\Rightarrow} \left(\begin{array}{rrr} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right)$$

到这一步，我们得到了 $K\subseteq \widetilde{K}$ 的群结构，下边借助 $\widetilde{W}$ 的泛性质，证明反包含关系 $\widetilde{K}\subseteq K$ 。

$\widetilde{W}$ 的泛性质

类似地，先用编程实验“知道”结论，再推导证明。

编程实验

1. 设群 $G=\langle X\rangle$，求 $G$ 关于生成元 $X$ 的泛性质。换言之，设 $F(X)$ 为集合 $X$ 上的自由群，求 $F(X)$ 子集 $R(X)$，使得

   $$F(X)/\overline{R(X)}\cong G$$

   其中 $\overline{R(X)}$ 为 $R(X)$ 生成的 $F(X)$ 的正规子群。

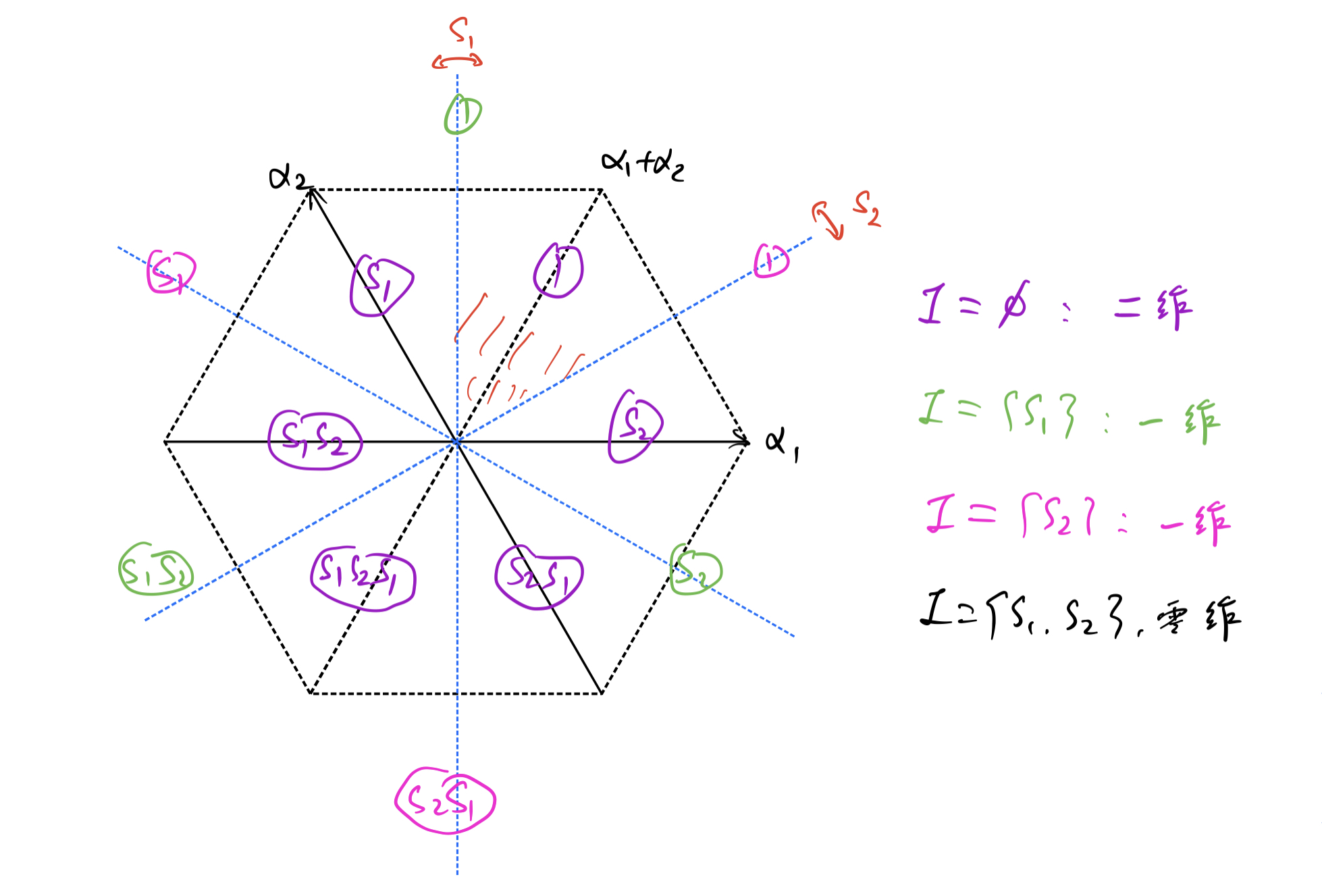
2. 用“群树”求解泛性质，叶子节点为泛性质等式，非叶子节点构成群树，以 $S_3=\langle s_1=(12),s_2=(23)\rangle$ 为例
   
   叶子节点给出粗糙的泛性质刻画，通过一些规则进一步简化，比如“删除子表达”
   

3. 比如 $A_3$ 情形

   reshape = lambda l,count=3:[flatten(l[count*i : count*(i+1)]) for i in range(ceil(len(l)/count))]
   # Universal property of Weyl group extension
   s,n = "A",3
   G = MatrixGroup(Thetas(s,n))
   relations = UniversalPropertyOfGroup(G,s="")
   relations_2 = [rel for rel in relations if len(rel[0])<2*4]
   relations_3 = [rel for rel in relations_2 if len(set(rel[0]+rel[1]))<3]
   relations_print = relations2element(relations_3,FreeGroup(n,"x").gens())
   table(reshape(relations_print))

   每行显示三个等式，比如划线处代表 $x_1x_0^2x_1=x_0^2$
   

4. 结合推导和实验，得出这几条性质：

   $$\begin{align*} (\theta_i\theta_j)^{o(s_is_j)}&= \begin{cases} \theta_i^2,& i=j\\ \theta_i^2\theta_j^2,& i\neq j,o(s_is_j)=2\\ \theta_i^2,& i\neq j,o(s_is_j)\neq 2,\vert\alpha_i\vert=\sqrt 2\vert\alpha_j\vert\\ 1,& otherwise \end{cases}&(1)\\ \theta_j\theta_i^2\theta_j^{-1}&=\begin{cases} \theta_i^2\theta_j^2& A_{ij}\ is\ odd\\ \theta_i^2& A_{ij}\ is\ even \end{cases}&(2)\\ \theta_i^2\theta_j^2&=\theta_j^2\theta_i^2,\ \forall\ i,j&(3)\\ \theta_1^{2\epsilon_1}\theta_2^{2\epsilon_2}\cdots\theta_n^{2\epsilon_n}&=1,\ (\epsilon_1,\epsilon_2,\cdots,\epsilon_n)A=0&(4) \end{align*}$$

注记，性质 (1)-(4) 的证明：

• 性质 (3)-(4) 上一小节已证
• 性质 (2) 借助 $\theta_ie_j$ 公式或 $\tau\theta_i\tau=\theta$ 证明
• 对有限族 EFG 族，性质 (1) 直接检验；对无限族 A-D 族，利用 $\widetilde{W}$ 的“局部性”化归为 $A_l(l\leq 4),B_l(2\leq l\leq 4),C_l(2\leq l\leq 4),D_l(4\leq l\leq 5)$ 再计算验证
• 实际上，(1)-(3) 以及前一节推导的公式，都可以利用局部性转化为有限情形的验证

理论推导

1. 先证明 $\widetilde{K}\subseteq K$，即证：

   $$\begin{align*} \left.\theta_{i_1}\cdots\theta_{i_k}\right|_H=\left.id\right|_H&\Rightarrow\theta_{i_1}\cdots\theta_{i_k}\in K\\ i.e.\quad s_{i_1}\cdots s_{i_k}=1&\Rightarrow\theta_{i_1}\cdots\theta_{i_k}\in K \end{align*}$$

   定义自由群 $F(S)$ 和 $F(\widetilde{S})$ 的子集如下：

   $$X = \{(s_is_j)^{o(s_is_j)}|\ \forall\ i,j\}\subseteq F(S)\\ \widetilde{X} = \{(\theta_i\theta_j)^{o(s_is_j)}|\ \forall\ i,j\}\subseteq F(\widetilde{S})$$

   由 Coxeter 群泛性质，左侧表达式写为

   $$s_{i_1}\cdots s_{i_k}=x_1^{y_1}\cdots x_r^{y_r},\ where\ x_i\in X,y_i\in W$$

   相应地，右侧式子化为

   $$\theta_{i_1}\cdots \theta_{i_k}=\tilde x_1^{\tilde y_1}\cdots \tilde{x}_r^{\tilde{y}_r},\ where\ \tilde x_i\in \widetilde X,\tilde y_i\in \widetilde W$$

   进而：

   $$\begin{aligned} equality\ (1)&\Rightarrow \tilde x_i\in K\\ equality\ (2)&\Rightarrow \tilde x_i^{\tilde y_i}\in K\\ &\Rightarrow\tilde x_1^{\tilde y_1}\cdots \tilde{x}_r^{\tilde{y}_r}\in K \end{aligned}$$

2. 下证性质 (1)-(4) 构成 $\widetilde{W}$ 的泛性质：
   设 $\theta_{i_1}\cdots \theta_{i_k}=1$，则

   $$\begin{aligned} As\ stated\ &before\\ &\theta_{i_1}\cdots \theta_{i_k}=\tilde x_1^{\tilde y_1}\cdots \tilde{x}_r^{\tilde{y}_r},\ where\ \tilde x_i\in \widetilde X,\tilde y_i\in \widetilde W\\ \theta_{i_1}\cdots\theta_{i_k} &\underset{reduces\ to}{\overset{(1)}{\Longrightarrow}}(\theta_{i_1,1}^2\cdots\theta_{i_1,i_{t_1}}^2)^{\tilde{y}_1}\cdots(\theta_{i_r,1}^2\cdots\theta_{i_r,i_{t_r}}^2)^{\tilde{y}_r}\\ &\underset{reduces\ to}{\overset{(2)}{\Longrightarrow}} \theta_{j_1}^2\cdots\theta_{j_t}^2\ \underset{reduces\ to}{\overset{(3)}{\Longrightarrow}} \theta_1^{2\epsilon_1}\cdots\theta_n^{2\epsilon_n}\ \underset{reduces\ to}{\overset{(4)}{\Longrightarrow}} 1 \end{aligned}$$

3. 最后，借助泛性质给出 $\widetilde{W}=K\rtimes_\sigma W$ 中的 2-cocycle $\sigma$:

   • 定义陪集映射 $\gamma$

     $$\begin{aligned} \gamma :W&\rightarrow \widetilde{W}\\ w=s_{i_1}s_{i_2}\cdots s_{i_k}&\mapsto \theta_{i_1}\theta_{i_2}\cdots \theta_{i_k} \end{aligned}$$

     其中 $s_{i_1}s_{i_2}\cdots s_{i_k}$ 为 $w$ 的简约表达，且按字典序取到极小。
   • 定义 $W$ 在 $K$ 上的作用：

     $$\begin{aligned} W&\rightarrow Aut(K)\\ w&\mapsto w:K\rightarrow K\\ &\qquad\quad\ \ x\mapsto \gamma(w)x\gamma(w)^{-1} \end{aligned}$$

   • 定义二上圈 $\sigma$

     $$\begin{aligned} \sigma :W\times W&\rightarrow K\\ (w_1,w_2)&\mapsto \gamma(w_1)\gamma(w_2)\gamma(w_1w_2)^{-1} \end{aligned}$$

   由泛性质知 $\sigma$ 右侧取值在 $K$ 上，且式子可借助 (1)-(4) 化简。

总结延伸

关于编程

编程起到的作用为：

• 计算数据，放大规律
• 提前思路，确认可行性，引导证明，避免思路跑偏
• 处理机械性的验证

延伸思考

1. $\widetilde{W}$ 的几何性质：

   • Weyl 群 $W$ 作用在 Cartan 子代数 $H$ 上，导出很多丰富的组合性质;类似地，$\widetilde{W}$ 在 $L$ 上的作用是否也有很好的性质。
   • $W\hookrightarrow Aut(\Phi)$ 作成正根系的置换；$\widetilde{W}\hookrightarrow (C_2)^n\rtimes_\sigma Aut(\Phi)$ 作成根系置换及符号变换，是否也有好的组合性质，比如定义 $s_{\pm\alpha_i}:=\theta_i^{\pm 1}$。

2. 观察发现，对于 ADE 族，$\widetilde{W}$ 作用在 $e_1$ 上，生成 Chevalley 基；对 BCFG 族，$\widetilde{W}$ 作用在 $e_1,e_n$ 上，生成 Chevalley 基。也即，给出 3-n 生成元后，借助 $\widetilde{W}$ 可生成一组 Chevalley 基。相关证明，及进一步的思考发散？

   # 检验 Chevalley 基性质
   def check(s,n):
       L = LieAlgebra(ZZ,cartan_type=[s,n])
       pos_num = (len(L.basis())-n)/2
       thetas = Thetas(s,n,reduced=True)
       for mat in MatrixGroup(thetas):
       mat = matrix(mat)
       if max(max(mat)) > 1 or min(min(mat)) < -1:
           return False
       return True
   test_data = [["G",[2]],["A",range(1,6)],["F",[4]],["B",range(2,6)],["C",range(2,6)],["D",range(4,6)]]
   for s,l in test_data:
       print(s)
       for n in l:
           print(check(s,n),end="\t")
       print()

   注：取不同 3-n 生成元，得到的 $\widetilde{W}$ 作为 $Inn(L)$ 子群未必相同。

3. 推导过程对于 Kac-Moody 代数也成立，相关的推广结论。